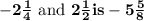Question

What is the product of −2 1/4 and 2 1/2?

Enter your answer as a mixed number, in simplified form, in the box.

Answer 1

-5 5/8

Explanation:

Answer 2

The product of
`\bold{-2 (1)/(4) \text { and } 2 (1)/(2) \text { is }-5 (5)/(8)}`

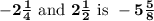
Solution:

From question, given that
`-2 (1)/(4) \text { and } 2 (1)/(2)`.

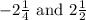We have to find the product of these fractions in terms of mixed number.

By converting mixed fraction to simple fraction,

`-2 (1)/(4) = -(9)/(4)`

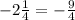
Similarly,

`2 (1)/(2) = (5)/(2)`

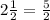
Hence the product of
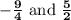`\bold{-(9)/(4) \text { and } (5)/(2)}` is

`= -(9)/(4) * (5)/(2)`

`= -(45)/(8)`

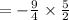
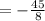
Now again convert
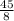`(45)/(8)` to mixed fraction,

When we divide 45 by 8, we get 5 as quotient and 5 as remainder. Here 8 is the divisor and 45 is the dividend.

The mixed fraction can be represented by,

`\bold{=q u o t i e n t (r e m a i n d e r)/(d i v i s o r)}`

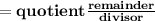
Hence
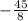`-(45)/(8)` in terms of mixed fraction can be written as
`-5 (5)/(8)`

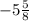
Hence product of
`\bold{-2 (1)/(4) \text { and } 2 (1)/(2) is-5 (5)/(8)}`