Answer:
The force of friction is 36.88 N
The coefficient of friction is 0.94
Step-by-step explanation:
Lets explain how to solve the problem
The force applied is 50 N rightward
The mass of the cart is 4 kg
The applied force makes the cart accelerate across a horizontal surface
The acceleration is 3.28 m/s²
We need to find the force of friction acting upon the cart
According to Newton's law
→ ∑ F in direction of motion = mass × acceleration
We have two horizontal forces acting on the cart
→ The force applied = 50 N
→ The force of friction
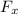in opposite direction of motion
→ The mass = 4 kg
→ Acceleration = 3.28 m/s²
Substitute these values in the rule
→ 50 -
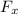= 4 × 3.28
→ 50 -
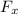= 13.12
Add
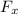for both sides
→ 50 =
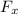+ 13.12
Subtract 13.12 from both sides
→ 36.88 =
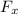
The force of friction is 36.88 N
→ The force of friction = μ R
where R is the normal reaction and μ is the coefficient of friction
→ R = mg
where m is the mass of the cart and g is the acceleration of gravity
→
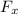= μ mg
→ g = 9.8 m/s² , m = 4 kg ,
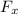= 36.88 N
Substitute these values in the rule
→ 36.88 = μ (4)(9.8)
→ 36.88 = 39.2 μ
Divide both sides by 39.2
→ μ = 0.94
The coefficient of friction is 0.94