Show that u(x,t)=cos(apix)e^-a^2pi^2t is a solution of the heat equation with k=1, on any interval [0,L].

Question

asked Dec 4, 2020 75.8k views

1 Answer

Logemann · Answer 1 · 2020-12-10T17:23:37+0000

Answer:

Explanation:

We have the function

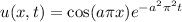$u(x,t) = \cos(a\pi x)e^(-a^2\pi^2t)$ ,

while the heat equation in one spacial dimension is

$(\partial u)/(\partial t) = (\partial^2 u)/(\partial^2 x)$ .

So, to solve this exercise we only need to calculate the derivatives that appears in the equation. Let us start by the derivative with respect to t:

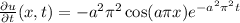$(\partial u)/(\partial t) (x,t) = -a^2\pi^2\cos(a\pi x)e^(-a^2\pi^2t)$ .

In the other hand

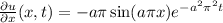$(\partial u)/(\partial x) (x,t) =-a\pi\sin(a\pi x)e^(-a^2\pi^2t)$ ,

then

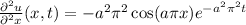$(\partial^2 u)/(\partial^2 x) (x,t) =-a^2\pi^2\cos(a\pi x)e^(-a^2\pi^2t)$ .

Notice that,

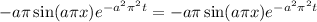
$-a\pi\sin(a\pi x)e^(-a^2\pi^2t)=-a\pi\sin(a\pi x)e^(-a^2\pi^2t)$

So, the function
satisfies the heat equation with
k=1 on any interval [0,L].