Answer: 104.026 m/s=374.49 km/h
Step-by-step explanation:
When a body or object falls, basically two forces act on it:
1. The force of air friction, also called "drag force"
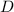 :
:
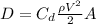 (1)
(1)
Where:
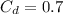 is the drag coefficient
is the drag coefficient
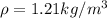 is the density of the fluid (air in this case)
is the density of the fluid (air in this case)
 is the velocity
is the velocity
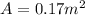 is the transversal area of the object
is the transversal area of the object
So, this force is proportional to the transversal area of the falling element and to the square of the velocity.
2. Its weight due to the gravity force
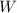 :
:
 (2)
(2)
Where:
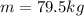 is the mass of the object
is the mass of the object
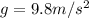 is the acceleration due gravity
is the acceleration due gravity
So, at the moment when the drag force equals the gravity force, the object will have its terminal velocity:
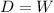 (3)
(3)
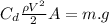 (4)
(4)
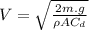 (5) This is the terminal velocity
(5) This is the terminal velocity
Substituting the known values in (5):
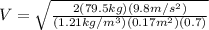 (6)
(6)
Then:
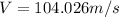 This is the final velocity in meters per second
This is the final velocity in meters per second
Now, let's find the final velocity in kilometers per hour, knowing
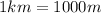 and
and
 :
:
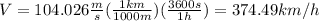 This is the final velocity in kilometers per hour.
This is the final velocity in kilometers per hour.