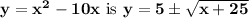Choose the inverse of y=x^2-10x

Question

asked May 28, 2020 147k views

2 Answers

Tracifycray · Answer 1 · 2020-06-04T18:01:23+0000

Answer:

Inverse of
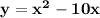$\bold{y=x^(2)-10 x}$ is
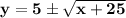
$\bold{y=5 \pm √(x+25)}$

Solution:

Given that

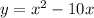
y=x^(2)-10 x

Adding
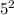5^(2) on both sides

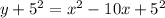
y+5^(2)=x^(2)-10 x+5^(2)

Rewrite 10x as 2(5)x,

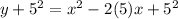
y+5^(2)=x^(2)-2(5) x+5^(2)

By using
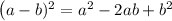$\left(a-b)^(2)=a^(2)-2 a b+b^(2)\right$ , we get

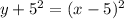
y+5^(2)=(x-5)^(2)

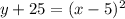y+25=(x-5)^(2) (Completing the square)

Now swap x and y, we get

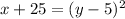
x+25=(y-5)^(2)

Rewrite the above equation,

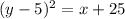
(y-5)^(2)=x+25

Taking square root of both sides,

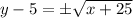
$y-5=\pm √(x+25)$

Adding 5 on both sides,

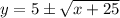
$y=5 \pm √(x+25)$

Hence inverse of
$\bold{y=x^(2)-10 x \text { is } y=5 \pm √(x+25)}$