Answer: The proof is given below.
Step-by-step explanation: Given that f and g are continuous on [a, b] and differentiable on (a, b). Also, f(a) = g(a) and f'(x) = g'(x) for a ≠ b.
We are to prove that
f(b) = g(b).
Cauchy Mean Vale Theorem: If p(x) and q(x) are any two functions that are continuous on [a, b] and differentiable on (a, b), then for some x in (a, b), we have
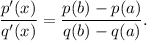
Since f(x) and g(x) satisfies the conditions of Cauchy Mean Value Theorem, so we get
![(f^\prime(x))/(g^\prime(x))=(f(b)-f(a))/(g(b)-g(a))\\\\\\\Rightarrow (f^\prime(x))/(f^\prime(x))=(f(b)-f(a))/(g(b)-f(a))~~~~~~~~~[\textup{since }f(a)=g(a)~\textup{and }f^\prime(x)=g^\prime(x)]\\\\\\\Rightarrow 1=(f(b)-f(a))/(g(b)-f(a))\\\\\Rightarrow f(b)-f(a)=g(b)-f(a)\\\\\Rightarrow f(a)=g(a).](https://img.qammunity.org/2020/formulas/mathematics/college/ymd2dzp4277dq75edxkf5ae15ial00a98z.png)
Thus, f(b) = g(b).
Hence proved.