Answer: The y-coordinate of the second car is -6.
Explanation:
Given : Two cars are traveling on two different roads that are perpendicular to each other.
Slope of first car started from the point (-5,-8) and stopped at (2,7):
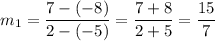
Slope of second car started at (-5,1) and stopped at (10,y) :
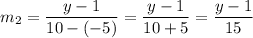
Since both cars perpendicular, then the product of their slope is equals to -1.
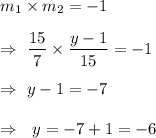
Hence, The y-coordinate of the second car is -6.