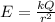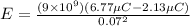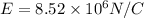Question

A solid conducting sphere of radius 2.00 cm has a charge of 6.77 μC. A conducting spherical shell of inner radius 4.00 cm and outer radius 5.00 cm is concentric with the solid sphere and has a charge of −2.13 μC. Find the electric field at the following radii from the center of this charge configuration. (a) r = 1.00 cm (b) r = 3.00 cm (c) r = 4.50 cm (d) r = 7.00 cm

Answer 1

Part a)

E = 0

Part b)

`E = 6.77 * 10^7 N/C`

Part c)

Electric field inside the conductor is again zero

`E = 0`

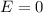
Part d)

`E = 8.52 * 10^6 N/C`

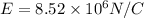
Step-by-step explanation:

Part a)

conducting sphere is of radius

R = 2 cm

so electric field inside any conductor is always zero

So electric field at r = 1 cm

E = 0

Part b)

Now at r = 3 cm

By Gauss law

`E = (kq)/(r^2)`

`E = ((9* 10^9)(6.77 \muC))/(0.03^2)`

`E = 6.77 * 10^7 N/C`

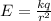
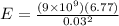
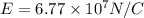
Part c)

Again when we use r = 4.50 cm

then we will have

Electric field inside the conductor is again zero

`E = 0`

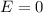
Part d)

Now at r = 7 cm

again by Gauss law

`E = (kQ)/(r^2)`

`E = ((9* 10^9)(6.77\mu C - 2.13\mu C))/(0.07^2)`

`E = 8.52 * 10^6 N/C`