Question

Which of the following statements is CORRECT? a. The present value of a 3-year, $150 annuity due will exceed the present value of a 3-year, $150 ordinary annuity. b. If a loan has a nominal annual rate of 8%, then the effective rate can never be greater than 8%. c. If a loan or investment has annual payments, then the effective, periodic, and nominal rates of interest will all be different. d. An investment that has a nominal rate of 6% with semiannual payments will have an effective rate that is smaller than 6%.

Answer 1

Statement a. is correct.

Step-by-step explanation:

The effective annual rate is always higher than the nominal interest rate, as the formula is clear for any number of periods, for any interest rate:

Effective Annual Rate of return =
`(1 + (i)/(n))^n - 1`

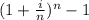
Further if we calculate the present value of annuity due and ordinary annuity assuming 6 % interest rate, then:

Present value of annuity due =

`(1 + 0.06) * 150 * ((1 - (1)/((1 + 0.06)^3) )/(0.06) )`

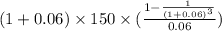
= 1.06
`*` $400.95

= $425.0089

Present value of ordinary annuity =
`150 * ((1 - (1)/((1 + 0.06)^3) )/(0.06) )`

= $150
`*` 2.6730

= $400.95

Therefore, value of annuity due is more than value of ordinary annuity.

Statement a. is correct.