Question

Two roommates share a dorm in Richards Hall, The probability that Roommate A is doing homework on a Friday night is .3. The probability that Roommate B is doing homework on a Friday night is .4. The probability that both roommates are doing homework on a Friday night is .2 (notice the two roommates are able to coordinate their decisions, so you can't assume their respective probabilities are independent). Find the probability that: At least one roommate is doing homework this Friday night

Answer 1

There is a 50% probability that at least one roommate is doing homework this Friday night.

Explanation:

This problem can be solved building the Venn Diagram of these probabilities.

I am going to say that P(A) is the probability that the roommate A is doing homework and P(B) is the probability that the roommate B is doing homework.

We have that:

`P(A) = P(a) + P(A \cap B)`

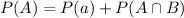
In which P(a) is the probability that only the roommate A is doing homework and
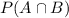`P(A \cap B)` is the probability that both student A and student B are doing homework.

We also have that:

`P(B) = P(b) + P(A \cap B)`

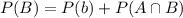
The problem states that

The probability that Roommate A is doing homework on a Friday night is .3. So
`P(A) = 0.3`.

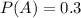The probability that Roommate B is doing homework on a Friday night is .4. So
`P(B) = 0.4`

The probability that both roommates are doing homework on a Friday night is .2. So
`P(A \cap B) = 0.2`

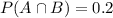
Find the probability that: At least one roommate is doing homework this Friday night

This is the probability that either only A is doing, either only B, or both. So:

`P = P(a) + P(b) + P(A \cap B)`

We have that

`P(A) = P(a) + P(A \cap B)`

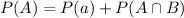
We have P(A) and
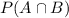`P(A \cap B)`, so we can find P(a)

`P(A) = P(a) + P(A \cap B)`

`0.3 = P(a) + 0.2`

`P(a) = 0.1`

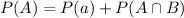
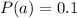
Also

`P(B) = P(b) + P(A \cap B)`

`0.4 = P(b) + 0.2`

`P(b) = 0.2`

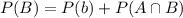
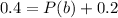
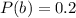
So:

`P = P(a) + P(b) + P(A \cap B)`

`P = 0.1 + 0.2 + 0.2`

`P = 0.5`

There is a 50% probability that at least one roommate is doing homework this Friday night.