Question

The trace of a square n x n matrix A = (a_ij) is the sum a11 + a22 +...+ ann of the entries on its main diagonal.Let V be the vector space of all 2 x 2 matrices with real entries. Let H be the set of all 2 x 2 matrices with real entries that have trace 0. Is H a subspace of the vector space V?Is H closed under addition? If it is, enter CLOSED. If it is not, enter two matrices in H whose sum is not in H, using a comma separated list and syntax such as [[????,????],[????,????]], [[????,????],[????,????]] for the answer [1324],[5768]. (Hint: to show that H is not closed under addition, it is sufficient to find two idempotent matrices ???? and ???? such that (????+????)2≠(????+????).)

Answer 1

Subspace; Closed

Explanation:

The trace of a square n x n matrix
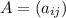`A = (a_(ij))` is the sum
`a_(11) + a_(22) +...+ a_(nn)` of the entries on its main diagonal.

Let V be the vector space of all 2 x 2 matrices with real entries.

Let H be the set of all 2 x 2 matrices with real entries that have trace 0.

Theorem: H is a subspace of the vector space V, if

1) for every
`A,\ B\in H: \ \ A+B\in H;`

2) for each
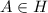`A\in H` and
`\lambda \in R:\ \ \lambda A\in H.`

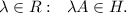
Check these two conditions:

1) Let
`A=(a_(ij)),\ B=(b_(ij))\in H`

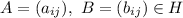
This means

`a_(11)+a_(22)=0\\ \\b_(11)+b_(22)=0`

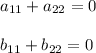
Consider the matrix
`A+B=(a_(ij)+b_(ij))=\left(\begin{array}{cc}a_(11)+b_(11)&a_(12)+b_(12)\\a_(21)+b_(21)&a_(22)+b_(22)\end{array}\right)`

This matrix sum has the trace

`(a_(11)+b_(11))+(a_(22)+b_(22))=(a_(11)+a_(22))+(b_(11)+b_(22))=0+0=0`

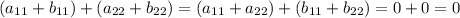
So,
`A+B\in H`

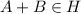
2) Consider
`\lambda A=\lambda\left(\begin{array}{cc}a_(11)&a_(12)\\a_(21)&a_(22)\end{array}\right)=\left(\begin{array}{cc}\lambda a_(11)&\lambda a_(12)\\\lambda a_(21)&\lambda a_(22)\end{array}\right)`

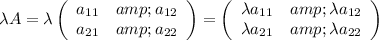
Its trace is
`\lambda a_(11)+\lambda a_(22)=\lambda (a_(11)+a_(22))=\lambda \cdot 0=0`

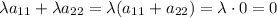
So,
`\lambda A\in H`

Therefore, H is a subspace of the vector space V and is closed under addition.