Question

The average performance rating of the employees at Company A is 6.5 on a scale from 1 to 10 (10 being highest). The standard deviation is 2.1 The average performance rating of the employees at Company C is 7.4. Company C has a standard deviation of 6.8. It would be better to hire a random employee from Company A.

Answer 1

The best choice would be hiring a random employee from company A

Explanation:

Supposing that the performance rating of employees follow approximately a normal distribution on both companies, we are interested in finding what percentage of employees of each company have a performance rating greater than 5.5 (which is the mean of the scale), when we measure them in terms of z-scores.

In order to do that we standardize the scores of both companies with respect to the mean 5.5 of ratings

The z-value corresponding to company A is

`z=(\bar x-\mu)/(s)`

where

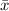`\bar x` = mean of company A

`\mu` = 5.5 (average of rating between 1 and 10)

s = standard deviation of company A

`z=(\bar x-\mu)/(s)=(6.5-5.5)/(2.1)=0.7142`

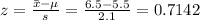
We do the same for company C

`z=(\bar x-\mu)/(s)=(7.4-5.5)/(6.8)=0.2794`

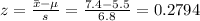
This means that 27.49% of employees of company C have a performance rating > 5.5, whereas 71.42% of employees of company B have a performance rating > 5.5.

So, the best choice would be hiring a random employee from company A