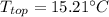Answer:
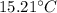
Step-by-step explanation:
We will use the the conservation of energy principle to solve this problem. In this sense, for the case of the Kerepakupai Vena waterfall the energy at the top must be equal to the energy at the bottom:
 (1)
(1)
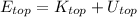 (2)
(2)
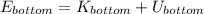 (3)
(3)
Where
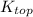 and
and
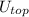 are the kinetic an potential energy at the top of the waterfall, respectively; and
are the kinetic an potential energy at the top of the waterfall, respectively; and
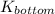 and
and
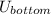 are the kinetic an potential energy at the bottom of the waterfall, respectively.
are the kinetic an potential energy at the bottom of the waterfall, respectively.
Since we are told the kinetic energy of the water is converted into thermal energy
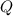 , we have:
, we have:
 and
and
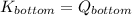
Hence (2) and (3) are rewritten as:
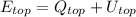 (4)
(4)
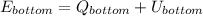 (5)
(5)
Then:
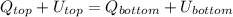 (6)
(6)
On the other hand we know the potential energy for both cases is:
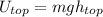 and
and
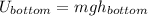
Where:
 is the mass of water
is the mass of water
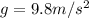 is the acceleration due gravity
is the acceleration due gravity
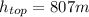 is the height at the top
is the height at the top
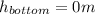 is the height at the bottom of the waterfall
is the height at the bottom of the waterfall
In addition, the thermal energy for both cases is:
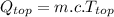 and
and
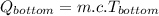
Where:
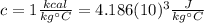 is the specific of water
is the specific of water
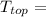 is the temperature at the top
is the temperature at the top
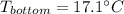 is the temperature at the bottom
is the temperature at the bottom
So, keeping this in mind, equation (6) is rewritten as:
 (7)
(7)
Since
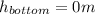 :
:
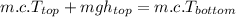 (8)
(8)
Finding
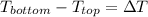 :
:
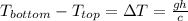 (9)
(9)
Solving:
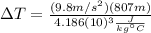 (10)
(10)
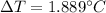 (11)
(11)
Now that we have
 and
and
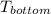 we can finally find
we can finally find
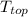 :
:
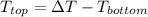 (12)
(12)
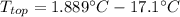 (13)
(13)
Therefore: