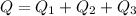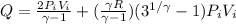Question

Your research group has developed a new type of engine, which is now undergoing laboratory tests. In the engine, a sample of an ideal gas with specific heat ratio γ is confined to a cylinder and carried through a closed cycle. The gas initially has pressure Pi, volume Vi, and temperature Ti. Its pressure is then tripled under constant volume. Then, it expands adiabatically to its original pressure. Finally, the gas is compressed isobarically to its original volume. What is the net work done by the engine for each cycle? (Use any variable or symbol stated above as necessary.)

Answer 1

Step-by-step explanation:

As we know that at isochoric conditions if pressure of the gas is tripled then the temperature also becomes 3 times

So heat given in this process is given as

`Q_1 = nC_v\Delta T`

`Q_1 = n((R)/(\gamma - 1))(3T_i - T_i)`

`Q_1 = (2P_iV_i)/(\gamma - 1)`

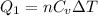
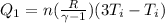
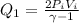
Now it is expanded to initial pressure again by adiabatic process

So in this part there is no heat exchange

`Q_2 = 0`

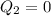
Also we know that

`(3P_i)^(1 - \gamma) (3T_i)^(\gamma) = (P_i)^(1 - \gamma)(T^(\gamma))`

`T = (3T_i)3^{(1 - \gamma)/(\gamma) = 3^(1/ \gamma)T_i`

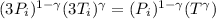
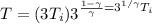
Now in the last process we compressed the gas to original volume

`Q_3 = nC_p\Delta T`

`Q_3 = n((\gamma R)/(\gamma - 1))(3^(1/ \gamma) T_i - T_i)`

`Q_3 = ((\gamma R)/(\gamma - 1))(3^(1 / \gamma) - 1)P_i V_i`

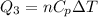
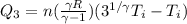
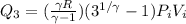
Now total heat in the process is given as

`Q = Q_1 + Q_2 + Q_3`

`Q = (2P_iV_i)/(\gamma - 1) + ((\gamma R)/(\gamma - 1))(3^(1 / \gamma) - 1)P_i V_i`