Question

In a jump spike, a volleyball player slams the ball from overhead and toward the opposite floor. Controlling the angle of the spike is difficult. Suppose a ball is spiked from a height of 2.10 m with an initial speed of 21.0 m/s at a downward angle of 14.0°. How much farther on the opposite floor would it have landed if the downward angle were, instead, 6.0°?

Answer 1

The ball would have landed 3.31m farther if the downward angle were 6.0° instead.

Step-by-step explanation:

In order to solve this problem we must first start by doing a drawing that will represent the situation. (See picture attached).

We can see in the picture that the least the angle the farther the ball will go. So we need to find the A and B position to determine how farther the second shot would go. Let's start with point A.

So, first we need to determine the components of the velocity of the ball, like this:

`V_(Ax)=V_(A)cos\theta`

`V_(Ax)=(21m/s)cos(-14^(o))`

`V_(Ax)=20.38 m/s`

`V_(Ay)=V_(A)sin\theta`

`V_(Ay)=(21m/s)sin(-14^(o))`

`V_(Ay)=-5.08 m/s`

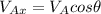
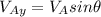
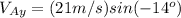
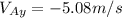
we pick the positive one, so it takes 0.317s for the ball to hit on point A.

so now we can find the distance from the net to point A with this time. We can find it like this:

`x_(A)=V_(Ax)t`

`x_(A)=(20.38m/s)(0.317s)`

`x_(A)=6.46m`

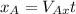
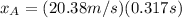
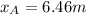
Once we found the distance between the net and point A, we can similarly find the distance between the net and point B:

`V_(Bx)=20.88 m/s`

`V_(By)=-2.195 m/s`

`y_(Bf)=y_(B0)+V_(0)t-(1)/(2)at^(2)`

`0=2.1m+(-2.195m/s)t-(1)/(2)(-9.8m/s^(2))t^(2)`

`-4.9t^(2)-2.195t+2.1=0`

`t=\frac{-b\pm\sqrt{b^(2)-4ac}}{2a}`

`t=\frac{-(-2.195)\pm\sqrt{(-2.195)^(2)-4(-4.9)(2.1)}}{2(-4.9)}`

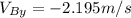
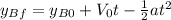
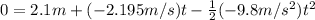
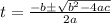
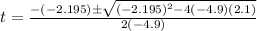
t= -0.9159s or t=0.468s

we pick the positive one, so it takes 0.468s for the ball to hit on point B.

so now we can find the distance from the net to point B with this time. We can find it like this:

`x_(B)=V_(Bx)t`

`x_(B)=(20.88m/s)(0.468s)`

`x_(B)=9.77m`

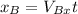
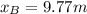
So once we got the two distances we can now find the difference between them:

`x_(B)-x_(A)=9.77m-6.46m=3.31m`

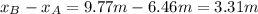
so the ball would have landed 3.31m farther if the downward angle were 6.0° instead.