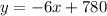Answer:
We can express the yield per tree as
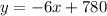
where y: yield per tree and x: number of trees, with x>75.
Explanation:
With this data we have that:
1) The annual yield per lemon tree is 330 pounds per tree when the number of trees per acre is 75
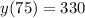
being y the yield per tree.
2) For each additional tree over 75, the annual yield per tree for all trees on the acre decreases by 6 pounds

being x the number of trees.
If we rearrange and integrate we have

If we use
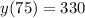 , we have
, we have
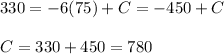
Then we can express the yield per tree as