Question

2. You have tested bearings for a particular machine. This resulted in a mean of 30,457,500 cycles with a standard deviation of 167,800 cycles (assume approximately normally distributed). (a.) What percentage of the bearings will last for 30,000,000 cycles? (b.) If the manufacturer is willing to accept a 5% failure rate, what warranty time should he put on the bearings?

Answer 1

(a) 99.68% of the bearings will last for 30,000,000 cycles

(b) The manufacturer should put 30,181,494 cycles of warranty time on the bearings

Explanation:

Let X be the random variable that represents the cycles of the bearings. We know that X is approximately normally distributed with a mean of
`\mu` = 30, 457, 500 cycles and a standard deviation of
`\sigma` = 167, 800 cycles. Then, we can assume that the normal probability density function for X is given by

`f(x) = \frac{1}{\sqrt{2\pi(167800)^(2)}}\exp[-((x-30457500)^(2))/(2(167800)^(2))]`

(a) To answer this question, we should to compute the next probability
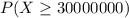`P(X\geq 30000000)`, i.e., the probability that the cycles of a bearing is equal or greater than 30,000,000.

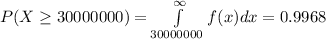`P(X\geq 30000000) = \int\limits_(30000000)^(\infty)f(x)dx = 0.9968`. So,

99.68% of the bearings will last for 30,000,000 cycles.

pnorm(30000000, mean = 30457500, sd = 167800, lower.tail = FALSE) (execute this in the R statistical programming language)

(b) We are looking for a value
`x_(0)` such that

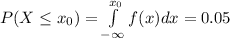`P(X\leq x_(0)) = \int\limits_(-\infty)^{x_(0)}f(x)dx = 0.05` and this value is
`x_(0)` = 30,181,494 cycles, i.e., we found the 5th percentile.

qnorm(0.05, mean = 30457500, sd = 167800) (execute this in the R statistical programming language)

You can use a table from a book to compute this figures or a programming language like the R statistical programming language.