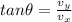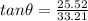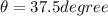Answer:
Part a)
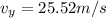
Part b)
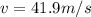
Part c)
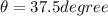
Step-by-step explanation:
Part a)
As we know that final velocity is
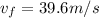
angle made by it is given as
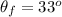
now we know its two components are
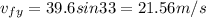
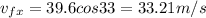
now we can use kinematics in Y direction
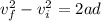
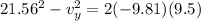
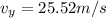
Part b)
Also we know that velocity in x direction will remains same
so

so net speed is given as
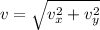
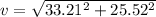
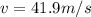
Part c)
Angle of projection is given as