Answer:
The inequality that you have is
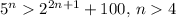 . You can use mathematical induction as follows:
. You can use mathematical induction as follows:
Explanation:
For
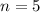 we have:
we have:
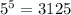
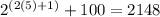
Hence, we have that
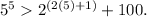
Now suppose that the inequality holds for
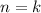 and let's proof that the same holds for
and let's proof that the same holds for
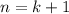 . In fact,
. In fact,
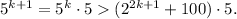
Where the last inequality holds by the induction hypothesis.Then,
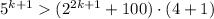
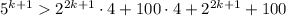
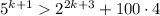
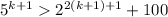
Then, the inequality is True whenever
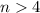 .
.