Question

. 100 people comprised of 75 women and 25 men have applied for promotions at local postal distribution facility. Only 6 of these 100 can be promoted. Also, since each of these 100 people are equally qualified to be promoted, management has decided to implement a lottery system so that each person has a equal chance to be promoted. (a) Compute the probability that no woman is promoted. Simplify completely - you’ll need a calculator. (b) Compute the probability that exactly 1 woman is promoted. Simplify completely - you’ll need a calculator. (c) If you observed at most one woman being promoted, would you suspect foul-play by management? Why?

Answer 1

(a) The probability of no women being promoted is 17%.

(b) The probability of only one women being promoted is 6%.

(c) The probability of having 2 women or more in the promotions is 32%, so it is not suspicious.

Explanation:

This is a case of combination (no replacement and order doesn't matter).

(a) The probability that no woman is promoted is equal to the probability of a man being choose for every promotion:

`P(no\, woman)=P(x_1=m)*P(x_2=m)*P(x_3=m)*P(x_4=m)*P(x_5=m)*P(x_6=m)\\\\P(no\, woman)=(75/100)*(74/99)*(73/98)*(72/97)*(71/96)*(70/95)\\\\P(no\, woman)=(1.45*10^(11))/(8.58*10^(11)) =0.17`

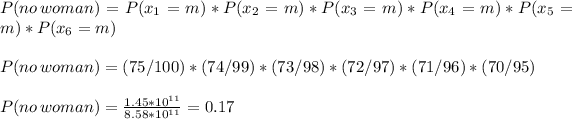
The probability of no women being promoted is 17%.

(b) The probability of only one woman being promoted is

`P(one\, woman)=P(x_1=w)*P(x_2=m)*P(x_3=m)*P(x_4=m)*P(x_5=m)*P(x_6=m)\\\\P(one\, woman)=(25/100)*(75/99)*(74/98)*(73/97)*(72/96)*(71/95)\\\\P(one\, woman)=(5.18*10^(10))/(8.58*10^(11)) =0.06`

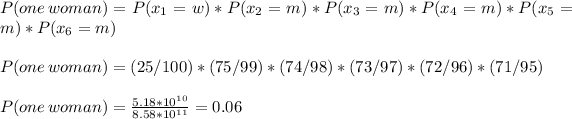
The probability of only one women being promoted is 6%.

(c) The expected number of women in the 6 promotions can be calculated as
`E(w)=p_w*6=(25/100)*6=1.5`.

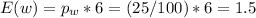This expected value, as approximated by a binomial distribution with p=0.25 (chances of picking a woman) and n=6, is

`\sigma=√(np(1-p))=√(6*0.25*0.75))=√(1.125)=1.06`

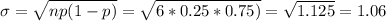
If we compute the z-value for 2 woman, and approximating by the central limit theorem, we can calculate the probability of this event.

`z=(x-\mu)/(\sigma)=(2-1.5)/(1.06)=  0.47`

Then P(z>-.47)=0.32 or 32%, what can be interpreted as the probability of having 2 or more women in the promotions.

We can conclude that it is not suspicious to have 2 women selected for promotions.