Step-by-step explanation:
Let the molar mass of KBr is
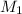 and NaBr is
and NaBr is
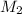 .
.
In 21.545 g, the moles of KBr and NaBr are
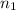 and
and
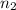 .
.
Therefore,
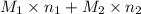 = 21.545 g
= 21.545 g
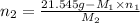
Mass of AgBr is 35.593 g.
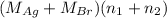 = 35.593 g
= 35.593 g
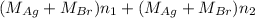 = 35.593 g
= 35.593 g
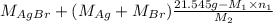 = 35.593 g
= 35.593 g

Now, putting the given values into the above formula as follows.

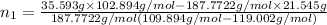
=
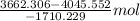
=

= 0.224 mol
Hence, mass of KBr will be calculated as follows.
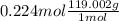
= 26.656 g
Thus, we can conclude that mass of KBr present in the original mixture is 26.656 g.