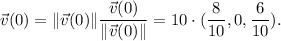Answer:
The particle's velocity is the derivative of the particle's position. The particles's acceleration is the derivative of the particle's velocity. You can compute the velocity and acceleration as follows:
Explanation:
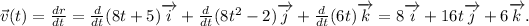
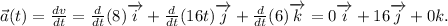
The velocity at
 is
is
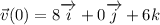 .
.
The speed at t=0 is
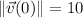 . Then, the velocity at t=0 written as a product of the speed at t=0 and the direction at t=0 is
. Then, the velocity at t=0 written as a product of the speed at t=0 and the direction at t=0 is