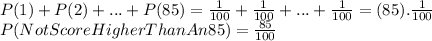Question

5. Bart is a student in a History class. In order for Bart to receive an A grade for the course, he must score higher than an 85 on the final exam (out of a possible 1 to 100 score). What is the probability that Bart will not score higher than an 85 and receive an A in the course ?

Answer 1

The probabability is
`(85)/(100) =0.850`

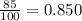
Explanation:

We are going to suppose that each score has the same probability.

For example :

`P(66) = P(89)`

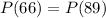
Where P(66) is the probability of score a 66 and P(89) is the probability of score an 89

If A is a certain score :

`P(A) = (CasesWhereAOccurs)/(Total Cases)`

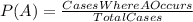
In the exercise :

`P(1) = P(2)=...=P(100)=(1)/(100) =0.01`

Bart must score higher than an 85 on the final exam.

We are looking for the probability of the event : ''Bart obtains a 1 or a 2 or ... or a 85''

This can be written in terms of events as :

P(1∪2∪...∪85) = P(1) + P(2) + ... + P(85)

As we consider each event as independent

`P(1) + P(2) + ... + P(85) =(1)/(100) +(1)/(100) +...+(1)/(100) =(85).(1)/(100) \\P(Not Score Higher Than An 85)=(85)/(100)`