Question

The manager of an automobile dealership is considering a new bonus plan designed to increase sales volume. Currently, the mean sales volume is 24 automobiles per month. The manager wants to conduct a research study to see whether the new bonus plan increases sales volume. To collect data on the plan, a sample of sales personnel will be allowed to sell under the new bonus plan for a one-month period.a. Which form of the null and alternative hypotheses most appropriate for this situation. H0: is (greater than or equal to 24/greater than 24/less than or equal to 24/less than 24/equal to 24/not equal to 24) Ha: is (greater than or equal to 24/greater than 24/less than or equal to 24/less than 24/equal to 24/not equal to 24)b. Comment on the conclusion when H0 cannot be rejected. (No evidence that the new plan increases sales./ The research hypothesis ? > 24 is supported; the new plan increases sales.)c. Comment on the conclusion when H0 can be rejected. (No evidence that the new plan increases sales./ The research hypothesis ? > 24 is supported; the new plan increases sales.)

Answer 1

The most appropriate null hypothesis for this situation is

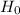`H_0`: The mean sales volume is equal to 24.

the most appropriate alternative hypothesis for this situation is

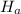`H_a`: The mean sales volume is greater than 24.

Explanation:

The null hypothesis
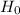`H_0` is the fact that is established and consider as true fact.

Since the established mean sales volume is 24 automobiles per month this should be considered as the null hypothesis.

So, the most appropriate null hypothesis for this situation is

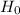`H_0`: The mean sales volume is equal to 24

The alternative hypothesis is a fact that intends to reject or refute the null by collecting data that could contradict it.

In this case, since the manager wants to conduct a research study to see whether the new bonus plan increases sales volume, he wants to see if the data collected after the new bonus plan can show that the new average is greater than the established one.

So, the most appropriate alternative hypothesis for this situation is

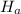`H_a`: The mean sales volume is greater than 24.

To try and prove that
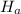`H_a` shows enough evidence as to assure the new plan actually increases sales volume, he must fix a significance level
`\alpha`, for example 0.1 or 0.05, which gives the probability that
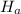`H_a` is not wrong in case that it rejects
`H_0`.

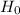This confidence level defines an
`\alpha`-score
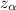`z_\alpha` which is a point such that the area under the normal curve N(0;1) to the right of
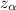`z_\alpha` is less than
`\alpha`.

In this case we considered the right side because you want to see the new average is greater than the established one.

If the z-score obtained through the sample is greater than
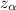`z_\alpha` then you can say the new bonus actually increases sales.

If the z-score obtained through the sample is less than or equals to
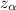`z_\alpha` then you do not have enough evidence showing that the new bonus actually increases sales.