Answer:
We fail to reject the null hypothesis that the bag filling machine works correctly at the 420 gram setting at the level of significance of 0.1. The p-value of the test statistic is 0.0250
Explanation:
We have the following null and alternative hypothesis
 vs
vs
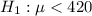 lower-tail alternative.
lower-tail alternative.
For n = 24,
 and
and
 .
.
 is normally distributed with a mean
is normally distributed with a mean
 and a standard deviation of
and a standard deviation of
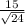 (approx). Therefore, we can use as test statistic
(approx). Therefore, we can use as test statistic
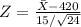 and the observed value is
and the observed value is
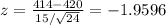
p-value = P(Z < -1.9596) = 0.0250
We can use a table from a book or a programming language to find this probability P(Z < -1.9596).
You can use the instruction pnorm(-1.9596) in the R statistical programming language.
Because the p-value is greater than 0.1 (0.0250 > 0.1) we fail to reject the null hypothesis at the level of significance of 0.1.