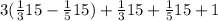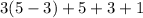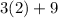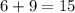Question

One-fifth of a swarm of bees is resting on a kadaba bush and a third on a silindha bush; three timesthe difference between these two numbers is on a kutaja, and a single bee has flown off in the breeze drawn by the odor of a jasmine and a pandam. Tell me, beautiful maiden, how many bees are there?

Answer 1

There are 15 bees.

Explanation:

Let's call x the total number of bees. There is one fifth of that in one bush, which can be written as:

`(1)/(5)x`

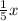
there is one third on another, which is:

`(1)/(3) x`

the other one has three times the difference between the previous two:

`3((1)/(3)x-(1)/(5)x)`

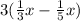
So, if we add those three quantities plus one single bee that flew away, it all should add up to the total number of bees, which is x. So:

`3((1)/(3)x-(1)/(5)x)+(1)/(3)x+(1)/(5)x+1=x`

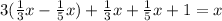
We will solve for x:

`(3)/(3)x-(3)/(5)x+(1)/(3)x+(1)/(5)x+1=x`

`(15)/(15)x-(9)/(15)x+(5)/(15)x+(3)/(15)x+1=x`

`(14)/(15)x+1=x`

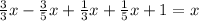
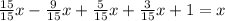
We will move the positive x on the right of the equal as a negative one to the left:

`(14)/(15)x-x+1=0`

`(14)/(15)x-(15)/(15)x+1=0`

`-(1)/(15)x+1=0`

`1=(1)/(15)x`

`15=x`

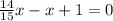
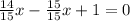
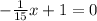
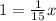
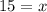
We can prove this answer by replacing in the original equation:

`3((1)/(3)15-(1)/(5)15)+(1)/(3)15+(1)/(5)15+1`

`3(5-3)+5+3+1`

`3(2)+9`

`6+9=15`