Question

In a solar water heater, energy from the Sun is gathered by water that circulates through tubes in a rooftop collector. The solar radiation enters the collector through a transparent cover and warms the water in the tubes; this water is pumped into a holding tank. Assume that the efficiency of the overall system is 28.0% (that is, 72% of the incident solar energy is lost from the system). What collector area is necessary to raise the temperature of 230 L of water in the tank from 20°C to 49°C in 2.6 h when the intensity of incident sunlight is 500 W/m2? The specific heat of water is 4186 J/kg·K. The density of water is 1.00 g/cm3.

Answer 1

21.30 m2

Step-by-step explanation:

First of all, we calculate the energy necessary to increase the temperature of the water from 20°C to 49°C. We use the specific heat in order to achieve this:

`Q = m_w*sh*(T_f-T_o)`

Where m_w is the mass of water, sh is the specific heat.

The mass of the water can be found using the volume of water and density:

`m_w = 230L_w * (1000 cm^3)/(1 L) *(1g)/(1cm^3) * (1kg)/(1000g) = 230 kg`

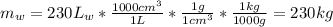
Then:

`Q = 230kg * 4186 J/kgK *(49^oC - 20^oC) =27 920 620 J = 27920.62 kJ`

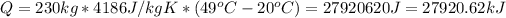
You want to heat the water in 2.6h, this means, you will need to supply a power equal to the total amount of energy required divided by the time in seconds. In 2.6h there are 2.6*3600 = 9360s:

`P =(27920620 J)/(9360s) = 2982.97 W`

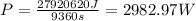
But remember, you have an efficiency of 28%, so the actual amount of power that you need to recieve from the sun is equal to:

`P_r = P/n = 2982.97 W/0.28 = 10653.47 W`

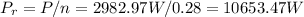
Now, for the power of a collector is:

`P_(sun) = S*A`

Where Psun is the power of the sun, S is the intensity of incident sunlight and A is the area. Solving for Area:

`A = P/S = (10653.47W)/(500W/m^2)=21.30 m^2`