Answer:
A) The expression for the number of bacteria is
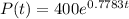 .
.
B) After 5 hours there will be 19593 bacteria.
C) After 5.55 hours the population of bacteria will reach 30000.
Explanation:
A) Here we have a problem with differential equations. Recall that we can interpret the rate of change of a magnitude as its derivative. So, as the rate change proportionally to the size of the population, we have

where
 stands for the population of bacteria.
stands for the population of bacteria.
Writing
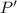 as
as
 , we get
, we get
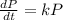 .
.
Notice that this is a separable equation, so
 .
.
Then, integrating in both sides of the equality:
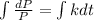 .
.
We have,
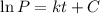 .
.
Now, taking exponential
 .
.
The next step is to find the value for the constant
 . We do this using the initial condition
. We do this using the initial condition
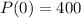 . Recall that this is the initial population of bacteria. So,
. Recall that this is the initial population of bacteria. So,
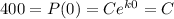 .
.
Hence, the expression becomes
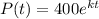 .
.
Now, we find the value for
 . We are going to use that
. We are going to use that
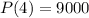 . Notice that
. Notice that
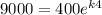 .
.
Then,
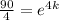 .
.
Taking logarithm
 , so
, so
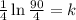 .
.
So,
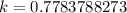 , and approximating to the fourth decimal place we can take
, and approximating to the fourth decimal place we can take
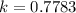 . Hence,
. Hence,
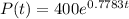 .
.
B) To find the number of bacteria after 5 hours, we only need to evaluate the expression we have obtained in the previous exercise:
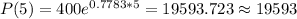 .
.
C) In this case we want to do the reverse operation: we want to find the value of t such that
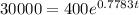 .
.
This expression is equivalent to
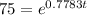 .
.
Now, taking logarithm we have
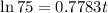 .
.
Finally,
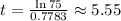 .
.
So, after 5.55 hours the population of bacteria will reach 30000.