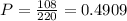Question

A pack of confectioneries contains candies in four (4) flavors (berry, lemon, orange and cacao), 3 pieces each. Candies are distributed randomly in the pack. You draw the first three (3) pieces from the pack. What is the probability that they are all different flavors?

Answer 1

The probability is 0.4909

Explanation:

The following equation for nCk give as the number of ways in which we can select k elements from a group of n elements:

`nCk=(n!)/(k!(n-k)!)`

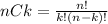
Then, there are 220 ways in which we can select 3 candies from the 12 that are in the pack. It is calculated as:

`12C3=(12!)/(3!(12-3)!)=220`

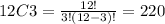
On the other hand, there are 108 different ways to select the 3 candies in which they are all different flavors. It is calculated as:

4C3 * 3C1 * 3C1 * 3C1 = 108

Because, 4C3 give us the number of ways to select 3 flavors from the 4 flavors. From this 3 flavors selected, we are going to select one candie from each one, so we multiply 3 times by 3C1, one for each flavor.

Finally, the probability is the division between the number of ways in which we can select 3 candies with different flavors and the total number of ways in which we can select 3 candies from the 12 in the pack. This is:

`P=(108)/(220)=0.4909`