Question

The work function of an element is the energy required to remove an electron from the surface of the solid element. The work function for lithium is 279.7 kJ/mol (that is, it takes 279.7 kJ of energy to remove one mole of electrons from one mole of Li atoms on the surface of Li metal). What is the maximum wavelength of light that can remove an electron from an atom on the surface of lithium metal?

Answer 1

Step-by-step explanation:

The given data is as follows.

Energy needed for 1 mole = 279.7 kJ =
`279.7 * (1000 J)/(1 kJ)`

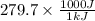
= 279700 J

Therefore, energy required for 1 atom will be calculated as follows.

`(279700)/(6.022 * 10^(22))`

=
`4.645 * 10^(-19) J`

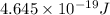
As relation between energy and wavelength is as follows.

E =
`(hc)/(\lambda)`

where, h = planck constant =
`6.62 * 10^(-34) Js`

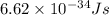
c = speed of light =
`3 * 10^(8) m/s`

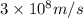
`\lambda` = wavelength

Therefore, putting given values into the above formula as follows.

E =
`(hc)/(\lambda)`

`4.645 * 10^(-19) J` =
`(6.62 * 10^(-34) Js * 3 * 10^(8) m/s)/(\lambda)`

`\lambda` =
`4.28 * 10^(-7) m`

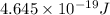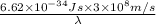
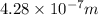
or, =
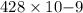`428 * 10{-9}` m

= 428 nm

Thus, we can conclude that the maximum wavelength of light that can remove an electron from an atom on the surface of lithium metal is 428 nm.