Answer:
The differential equation is not exact.
Explanation:
We can write the differential equation as
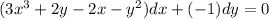
with
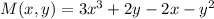
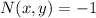
to check whether the differential equation is exact, we must verify that
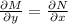
But
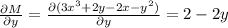
whereas

and we can see
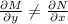
So the differential equation is not exact.