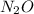Answer:
In 12.6g of
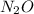 there are 0.29 moles of
there are 0.29 moles of
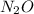 and
and
 molecules of
molecules of
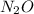
Step-by-step explanation:
First you should find the molar mass of the
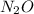 :
:
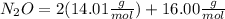
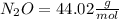
Then you should write the conversion factor using the molar mass:
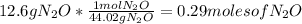
So, there are 0.29 moles of
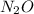 in 12.6g of
in 12.6g of
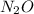 .
.
Finally to find the number of molecules, you should use the Avogadro´s number:
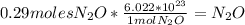
There are
 moles of
moles of
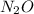 in 12.6g of
in 12.6g of