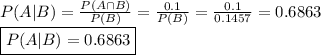Question

Guests at the White House have to clear four layers of security by the secret service: two identity checks, a dog sniff check, and a metal detection check with an X-ray machine. Historically 16% of the people in line are tourists and the rest are guests. All tourists are filtered out at the identity checkpoints, so they are not going through the dog and X-ray checkpoints. The dog check results in an alarm for 20% of the people in line. Guests who trigger a dog alarm also trigger an X-ray alarm with probability 1/10. Guests who do not trigger a dog alarm trigger an X-ray alarm with probability 1/16. What is the probability that a guest who triggers an X-ray alarm also triggers a dog alarm?

Answer 1

0.6863

Explanation:

Let A and B be the events

A = the dog check alarm is triggered

B= the x-ray alarm is triggered

As guests who trigger a dog alarm also trigger an x-ray alarm with probability 1/10, we have P(A∩B) = 0.1 .

The dog alarm can only be triggered by a guest, so we want to find P(A|B) , the probability that a guest triggers the dog alarm given that she triggered the x-ray alarm.

But

`P(A|B)=(P(A \cap B))/(P(B))=(0.1)/(P(B))`

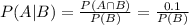
So we only need to find P(B) to find P(A|B) out.

Since 16% of people (tourists) in line are filtered out before reaching the dog alarm, only 84% of people (guests) reach the dog alarm. That is to say, 16% of 84% = 13.44% of people in line reach the dog alarm.

Since the dog check results in an alarm for 20% of the people in line, 20% of 13.44% = 2.688% of people in line (guests) trigger the dog alarm, so

P(A) = 0.02688.

Since guests who do not trigger the dog alarm trigger an X-ray alarm with probability 1/16, we have P(B|
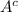`A^c`) = 0.0625.

We have then the following:

`P(B|A^c)=(P(B\cap A^c))/(P(A^c))=0.0625 \Rightarrow P(B\cap A^c)=0.0625P(A^c)=0.0625(1-P(A))=0.0625(1-0.2688)=0.0457`

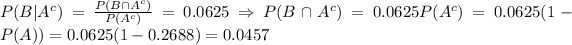
But
`A \cap B` and
`A^c \cap B` are disjoints sets whose union is B, so

`P(B)=P((A\cap B)\cup(A^c\cap B))=P(A\cap B)+P(A^c\cap B)=0.1+0.0457=0.1457`

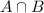and finally

`P(A|B)=(P(A \cap B))/(P(B))=(0.1)/(P(B))=(0.1)/(0.1457)=0.6863 \\ \boxedP(A`