Question

011

To win the game, a place kicker must kick a football from a point 45 m (49.212 yd) from the goal, and the ball must clear the crossbar, which is 3.05 m high. When kicked, the ball leaves the ground with a speed of 24 m/s at an angle of 32.6 ◦ from the horizontal. The acceleration of gravity is 9.8 m/s 2 . By how much vertical distance does the ball clear the crossbar? Answer in units of m.

Answer 1

In order to win the game of football, player has to kick the ball at a distance of 45 m from the goal which must cross the bar at 3.05 m of height. The vertical distance by which the ball clears the cross bar is 1.65 metres.

Answer: 1.65 metre

Step-by-step explanation:

Given, velocity = 24 m/s, angle of projectile= 32.6 degrees and acceleration = 9.8
`m / s^(2)`

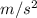
To know the height, we first need to know the velocity component,

`v_(x)=24 \sin 32.6^(\circ)=12.9 \mathrm{m} / \mathrm{s}`

`v_(y)=24 \cos 32.6^(\circ)=20.2 \mathrm{m} / \mathrm{s}`

The time travelled by the ball =
`\frac{\text { distance travelled }}{\text {velocity in the direction of travel}}=(45)/(20.2)=2.2 \mathrm{sec}`

From the equation of motion,

`s_(y) = v_(y) t+(1)/(2) a t^(2)`

=
`12.9 * 2.2+(1)/(2)-9.8 * 2.2 * 2.2`

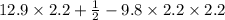
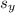`s_(y)` = 4.7 m.

Therefore, the vertical distance by which all ball clears the cross bar = ball height – cross bar height = 4.7 – 3.05 = 1.65 metre.