Answer:
a)V=17.76 cm/s
b)V=22.44 cm/s
c)V=50.49 cm/s
d)V=35.06 cm/s
e)V=37.63 cm/s
Step-by-step explanation:
Given that
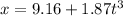
a)
When t= 2 s
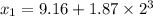

When t= 3 s
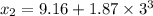
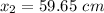
So the average velocity V
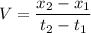
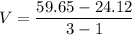
V=17.76 cm/s
b)
When know that
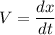
So
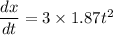
When t= 2 s
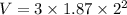
V=22.44 cm/s
c)
At t= 3 s
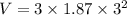
V=50.49 cm/s
d)
At t= 2.5 s
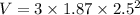
V=35.06 cm/s
e)
At t= 2 s ,x=24.12 cm
At t=3 s x=59.65 cm
So midway of 24.12 cm and 59.65 cm is (24.12+59.65 )/2=41.88 cm
So when x=41.88 cm
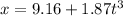
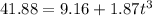
t=2.59 s
So velocity
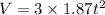
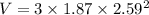
V=37.63 cm/s