Question

Jessica Salas, president of Salas Products, is reviewing the warranty policy for her company's new model of automobile batteries. Life tests performed on a sample of 100 batteries indicated: (1) an average life of 75 months, (2) a standard deviation of 5 months, and (3) a bell shaped battery life distribution. What percentage of the batteries will fail within the first 65 months of use

Answer 1

2.28% of the batteries will fail within the first 65 months of use

Explanation:

We have a bell shaped battery life distribution. Let X be the random variable that represents a battery life in months. If we suppose that we can model the battery lifes with the normal distribution with
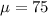`\mu = 75` months and
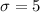`\sigma = 5` months, we have the normal probability density function

`f(x) = \frac{1}{\sqrt{2\pi(5)^(2)}}\exp[-((x-75)^(2))/(2(5)^(2))]`,

we are seeking
`P(X \leq 65)`.

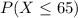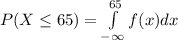`P(X \leq 65) = \int\limits_(-\infty)^(65) f(x) dx` = 0.0228. So

2.28% of the batteries will fail within the first 65 months of use. We can use a table from a book or a programming language to compute the probability, here we use the instruction pnorm(65, mean = 75, sd = 5) and the R statistical programming language.