Question

In class, Julie was asked to create a scenario for the linear function shown. She came up with the following: (image below)

Joe planned a hiking trip from where he parked his car to the mountain cabin he had rented. Joe parked 12 miles away from the cabin. After one hour, he was still 7 miles from the cabin. Joe’s hike from his car to the cabin can be modeled by the function f(x)=-3x+12.

Does Julie’s scenario match the linear function graphed? If not, where does she go wrong? How can she correct her mistake and match scenario to the function?

Answer 1

The graph that Julie drew is wrong, I don't know where she went wrong but the graph should look like this: (image shown below)

Answer 2

Yes, she made a mistake in the statement "after one hour, Joe was still 7 miles from the cabin". She should write 9 instead of 7 in that statement.

Explanation:

If a line passes through two points
`(x_1,y_1)` and
`(x_2,y_2)`, then the equation of line is

`y-y_1=(y_2-y_1)/(x_2-x_1)(x-x_1)`

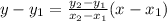
The given graph passes through the point (0,12) and (4,0). So, the equation of line is

`y-12=(0-12)/(4-0)(x-0)`

`y-12=-3x`

`y=-3x+12`

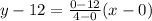
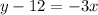
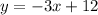
Therefore the graph represented by the equation y=-3x+12.

The initial value of the function is 12. The value of function after one unit is

`y=-3(1)+12=9`

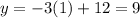
In her scenario she write that after one hour, joe was still 7 miles from the cabin.

7 ≠ 9

So, she made a mistake in her scenario. She should write 9 instead of 7 in her scenario.