Question

from the edge of a 486-foot cliff, peyton shot an arrow over the ocean with an initial upward velocity of 90-feet per second

Answer 1

9 seconds

Explanation:

The complete question is

The altitude of an object, d, can be modeled using the equation below:

d=-16t^2 +vt+h

from the edge of a 486 foot cliff, Peyton shot an arrow over the ocean with an initial upward velocity of 90 feet per second. In how many seconds will the arrow reach the water below?

Let

d ----> the altitude of an object in feet

t ---> the time in seconds

v ---> initial velocity in ft per second

h ---> initial height of an object in feet

we have

`d=-16t^2 +vt+h`

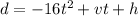
we know that

When the arrow reach the water the value of d is equal to zero

we have

`v=90\ ft/sec`

`h=486\ ft`

`d=0\ ft`

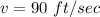
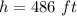
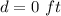
substitute the values and solve for t

`0=-16t^2 +(90)t+486`

`-16t^2+90t+486=0`

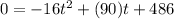
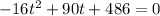
Multiply by -1 both sides

`16t^2-90t-486=0`

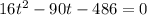
The formula to solve a quadratic equation of the form
`ax^(2) +bx+c=0` is equal to

`x=\frac{-b(+/-)\sqrt{b^(2)-4ac}} {2a}`

in this problem we have

`a=16\\b=-90\\c=-486`

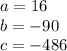
substitute in the formula

`t=\frac{90(+/-)\sqrt{-90^(2)-4(16)(-486)}}{2(16)}`

`t=(90(+/-)√(39,204))/(32)`

`t=(90(+/-)198)/(32)`

`t_1=(90(+)198)/(32)=9\ sec`

`t_2=(90(-)198)/(32)=-3.375\ sec`

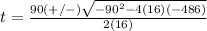
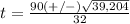
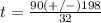
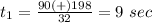
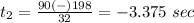
the solution is t=9 sec

see the attached figure to better understand the problem