Question

A parallel-plate capacitor with plates of area 720 cm2 is charged to a potential difference V and is then disconnected from the voltage source. When the plates are moved 0.5 cm farther apart, the voltage between the plates increases by 100 V. What is the charge Q on the positive plate of the capacitor?

Answer 1

`Q=1.27* 10^(-8)\ C`

Step-by-step explanation:

Given that,

Area of the parallel plate,
`A=720\ cm^2=0.072\ m^2`

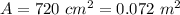
Separation between two plates,
`\Delta d=0.5 cm = 0.5* 10^(-2)\ m^2`

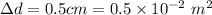
Voltage between the plates,
`\Delta V=100\ V`

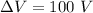
Let Q is the positive charge on the capacitor and
`\sigma` is the surface charge density. It cane be given by :

`Q=\sigma A`

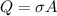
The relation between electric field and the surface charge density is given by :

`\sigma=\epsilon_oE`

Also,
`E=(\Delta V)/(\Delta d)`

So,
`Q=(\epsilon_o A\Delta V)/(\Delta d)`

`Q=(8.85* 10^(-12)* 0.072* 100)/(0.5* 10^(-2))`

`Q=1.27* 10^(-8)\ C`

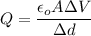
So, the charge on the positive plate of the capacitor is
`1.27* 10^(-8)\ C`. Hence, this is the required solution.