Answer: $50,846.3701
Step-by-step explanation:
Need to save $4 million to live comfortably,
Interest rate, r = 3%
N = 40 years
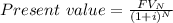
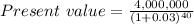
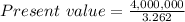
= 1,226,241.57

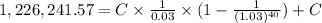
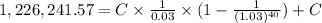
![1,226,241.57=C[(1)/(0.03)*(1-0.3065)+1]](https://img.qammunity.org/2020/formulas/business/college/8elg7uzjtq6vq7yqjirbpudgovodipnuw4.png)
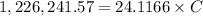
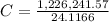
= $50,846.3701
Hence, $50,846.3701 will be the annual payment to have $4 million in the account on 65th birthday.