Question

used to flavor vanilla ice cream and other foods) is the substance whose aroma the human nose detects in the smallest amount. The threshold limit is 2.0 x 10-11 g per liter of air. If the current price of 50.0 g of vanillin is $104, determine the cost to supply enough vanillin so that the aroma could be detected in a large aircraft hangar with a volume of 5.95 x 107 ft. Guided Solution

Answer 1

The cost to supply enough vanillin so that the aroma could be detected in a large aircraft hangar with a volume of 5.95 x 10^7 ft^3 is $ 0.07.

Explanation:

The volume of the hangar is

`V=5.95*10^7 \, ft^3`

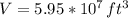
The minimal amount of vainilla needed to be detected in the hangar is equivalent to the threshold multiplied by the volume of the hangar:

`Va=V*Th=5.95*10^7 \, ft^3*2.0*10^(-11)\,(g)/(L)*(28.317L)/(1ft^3)\\  \\Va=336.9723*10^(-4) \, g=0.0337\,g`

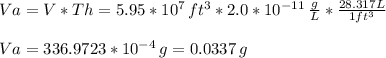
The cost of this amount of vainilla is

`Cost = Va*p=0.0337\,g*(104\, usd)/(50\, g) =0.07 \, usd`

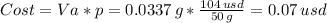
The cost to supply enough vanillin so that the aroma could be detected in a large aircraft hangar with a volume of 5.95 x 10^7 ft^3 is $ 0.07.