Question

The pressure in an automobile tire depends on the temperature of the air in the tire. When the air temperature is 25°C, the pressure gage reads 210 kPa. If the volume of the tire is 0.025 m3, determine the pressure rise in the tire when the air temperature in the tire rises to 50°C. Also, determine the amount of air that must be bled off to restore pressure

Answer 1

Answer:0.0704 kg

Step-by-step explanation:

Given

initial Absolute pressure
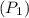`(P_1)`=210+101.325=311.325

`T_1=25^(\circ)\approx 298 K`

`V=0.025 m^3`

`T_2=50^(\circ)\approx 323 K`

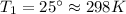
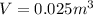
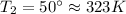
as the volume remains constant therefore

`(P_1)/(T_1)=(P_2)/(T_2)`

`(311.325)/(298)=(P_2)/(323)`

`P_2=337.44 KPa`

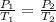
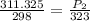
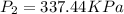
therefore Gauge pressure is 337.44-101.325=236.117 KPa

Initial mass
`m_1=(P_1V)/(RT_1)=(311.325* 0.025)/(0.0287* 298)`

`m_1=0.91 kg`

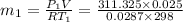
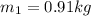
Final mass
`m_2=(P_2V)/(RT_2)=(311.325* 0.025)/(0.0287* 323)`

`m_2=0.839`

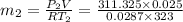
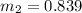
Therefore
`m_1-m_2`=0.91-0.839=0.0704 kg of air needs to be removed to get initial pressure back