Question

Air enters a well-insulated turbine operating at steady, state with negligible velocity at 4 MPa, 300°C. The air expands to an exit pressure of 100kPa. The exit velocity and temperature are 90 m/s and 100°C, respectively. The diameter of the exit is 0.6 m. Determine the power developed by the turbine (in kW). You may assume air behaves like an ideal gas throughout the process

Answer 1

-3744.45 kW

Step-by-step explanation:

The energy balance for a turbine is the following:

`U_(e)+P_(e)*v_(e)+gz_(e)+(C_(e)^(2))/(2)+q=W+U_(s)+P_(s)*v_(s)+gz_(s)+(C_(s)^(2))/(2)`

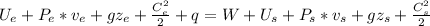
Where:

U = internal energy, P= pressure, v=volume, g= gravity, z= height, C= velocity, q= heat, W= power.

Since it is a well-insulated turbine q= 0.

In steady state m (mass flow) is constant.

`m=(1)/(v_(s))*A*C`

Where
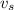`v_(s)` is the specific volume and A = area.

There is no information about a change in height during the process so we can say that the term (gz) in the equation both in the inlet (e) and outlet (s) is zero.

In the inlet the velocity is negligible so
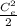`(C_(e)^(2))/(2)` is zero.

Also, enthalpy (h) is:

`h=U+P*v`

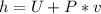
Reorganizing the equation with this information we have

`h_(e) =W + h_(s) +(C_(s)^(2))/(2)`

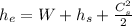
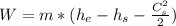`W= m*(h_(e)- h_(s)-(C_(s)^(2))/(2))` in kW

We can get the enthalpy from thermodynamic tables for the air with the conditions in the inlet and in outlet. These are:

`h_(e) (300 C) = 578.81 (kJ)/(kg)`

`h_(s) (100 C) = 273.26 (kJ)/(kg)`

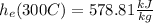
Mass flow

The area is the area of the circle
`A=pi()*r^(2)`

`A=pi()*(0.3m)^(2)=0.282 m^(2)`

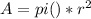
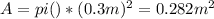
We can get the specific volume from thermodynamics tables for air at 100°C. We use this condition because we know the diameter and the velocity in the outlet. This value is

1.057
`(m^(3))/(kg)`

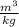
Mass flow is

`m=(1)/(1.057(m^(3))/(kg)) * 0.282 m^(2)* 90(m)/(s)=24.072 (kg)/(s)`

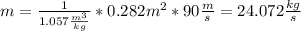
So power is:

`W= 24.072 (kg)/(s)*(578.81 (kJ)/(kg)-273.26 (kJ)/(kg)+((90(m)/(s))^(2))/(2)=-3744.45 Kw`