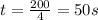Question

A 200-m-wide river flows due east at a uniform speed of 2.0 m/s. A boat with a speed of 8.0 m/s relative to the water leaves the south bank pointed in a direction 30° west of north. What are the (a) magnitude and (b) direction of the boat’s velocity relative to the ground? (c) How long does the boat take to cross the river?

Answer 1

Step-by-step explanation:

Given

Width of river=200 m

Speed of river
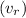`(v_r)`=2 m/s

Speed of Boat relative to river
`(v_(br))`=8 m/s

Boat leaves the bank
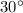`30^(\circ)` west of north

`v_(br)=-8cos30\hat{i}+8sin30\hat{j}`

`v_(r)=2\hat{i}`

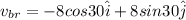
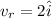
Therefore velocity of boat w.r.t ground

`v_b=v_(br)+v_r=-8cos30\hat{i}+8sin30\hat{j}+2\hat{i}`

`v_b=-4.928\hat{i}+4\hat{j}`

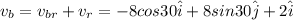
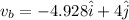
Magnitude of boat speed
`=√(4.928^2+4^2)=6.34 m/s`

For direction

`tan\theta =(4)/(4.928)`

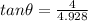
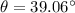`\theta =39.06^(\circ)` w.r.t to west

to cross the river its north component will help so

time taken
`t=(200)/(4)=50 s`