Question

If the composition of two functions is:

1/x-3

What would be the domain restriction? Describe how you found that answer.
[No Answer Choices]
I'm pretty sure the answer would be x≠3, because typically in these scenarios, anything the x on the bottom is being subtracted by has that symbol and the number being subtracted from it. I believe this is because x is = to 3, meaning that - 3 would make it 0 again. Thus, x≠3. But if this isn't true, I'd like someone else to explain it to me, and provide me with the correct answer.

Answer 1

R-{3}

Explanation:

Given is a function

`f(x) = (1)/(x-3)`

The domain is the possible values which x can take

Here on analysing the function we find that f(x) becomes undefined when denominator =0

i.e.
`x-3 \\eq 0\\x\\eq 3`

There cannot be any other restriction as there is no square root sign.

Hence domain is set of all real numbers except 3

In interval notation domain =
`(-\infty, 3)U(3,\infty)`

Answer 2

You are correct! The problems that can arise with a function domain are:

• Denominators that become zero
• Even-degree roots with negative input
• Logarithms with negative or zero input

In this case, you have a denominator, and you don't have roots nor logarithms. This means that your only concern must be the denominator, specifically, it cannot be zero.

And you simply have

`x-3\\eq 0 \iff x \\eq 3`

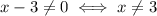
So, the domain of this function includes every number except 3.