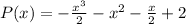Question

The polynomial of degree 3 , P ( x ) , has a root of multiplicity 2 at x = 1 and a root of multiplicity 1 at x = − 4 . The y -intercept is y = − 2

Answer 1

Explanation:

correct homie

Answer 2

`P(x)=-(x^3)/(2)-x^2-(x)/(2)+2`

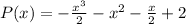
Explanation:

A polynomial can be written as:

`P(x)=a*(x-x_1)^t*(x-x_2)^v*...*(x-x_n)^w`

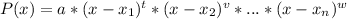
Where
`a` is the lead coefficient. And
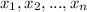`x_1,x_2,...,x_n` are the roots of the polynomial.

And
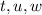`t,u,w` are the orders of multiplicity.

The polynomial has degree 3 and it has 2 factors, this is:

`P(x)=a*(x-x_1)^t*(x-x_2)^v`

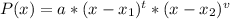
We have a root of multiplicity 2 at x = 1, then:

`(x-x_1)^t=(x-1)^2`

And we have a root of multiplicity 1 at x = − 4:

`(x-x_2)^v=(x-(-4))^1=(x+4)`

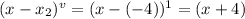
Then,
`P(x)=a*(x-1)^2*(x+4)`

And the problem says that the y-intercept is y=-2 this means that when x=0, y=-2

Observation: P(x)=y

Now we have to replace P(x) with x=0:

`P(x)=a*(x-1)^2*(x+4)\\P(0)=a*(0-1)^2*(0+4)\\\\-2=4a\\a=-(1)/(2)`

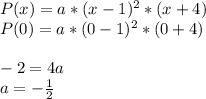
Then
`P(x)=-(1)/(2) *(x-1)^2*(x+4)`

`P(x)=-(1)/(2)(( x^2-2x+1)*(x+4))\\\\P(x)=-(1)/(2)(x^3+4x^2-2x^2+x+4)\\\\P(x)=-(1)/(2)(x^3+2x^2+x+4)\\\\P(x)=-(x^3)/(2)-x^2-(x)/(2)+2`

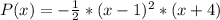
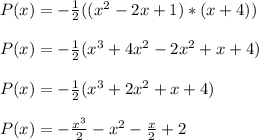
You can see that the polynomial is of degree 3.

The result is
`P(x)=-(x^3)/(2)-x^2-(x)/(2)+2`