Question

Find the average rate of change for f(x)=x+6 over the interval [4,8]

Answer 1

The Average rate of change for f(x) = x+6 over the interval (4,8) is 1

Solution:

We define the Average rate of function f(x) over the interval (a, b) as

`(f(b)-f(a))/(b-a)` --- eqn 1

From question, given that

f(x) =x+6 --- eqn 2

The interval is (4,8) .hence we say a = 4 and b = 8

The average rate of change for f(x) = x + 6 is given by using eqn 1

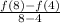`(f(8)-f(4))/(8-4)` --- eqn 3

Where, by using eqn 2 , we get f(8) = 8+6 =14 and f(4) = 4+6 =10

Such that the required value would be f(8)-f(4) = 14-10 = 4

By substituting the values of f(8) and f(4) in eqn 3 ,the average rate of change for the given expression is

`=(14-10)/(8-4)=(4)/(4)=1`

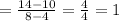
Hence the Average rate of change for f(x) = x+6 over the interval (4,8) is 1

Answer 2

Solve for f(x) using both 4 and 8:

f(x) = 4+6 = 10

f(x) = 8+6 = 14

Find the difference between the answers:

The difference between the two answers is 14-10 = 4

Find the difference between the interval:

The difference between 4 and 8 is: 8-4 = 4

The rate of change is the change in the answers over the difference in the interval:

The rate of change is 4/4 = 1