Question

Given ΔMNO, find the measure of ∠LMN.

Triangle MNO with segment LM forming a straight angle with segment MO and segment OP forming a straight angle with segment MO, the measure of angle NOP is 104 degrees, and segment MN and NO are marked congruent.

38°
52°
76°
104°

Answer 1

Option D.

Explanation:

Given information: MN ≅ NO

Isosceles triangle property : If two sides of a triangle and congruent then the angles opposite those sides are congruent.

Using Isosceles triangle property we get

`\angle NMO\cong \angle NOM`

Segment LM forming a straight angle with segment MO.

`\angle LMN+\angle NMO=180`

`\angle NMO=180-\angle LMN`

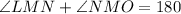
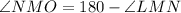
Segment OP forming a straight angle with segment MO.

`\angle NOP+\angle NOM=180`

`\angle NOM=180-\angle NOP`

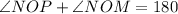
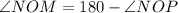
Since
`\angle NMO\cong \angle NOM`, so

`180-\angle LMN\cong 180-\angle NOP`

`\angle LMN\cong \angle NOP`

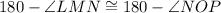
It is given that measure of angle NOP is 104 degree.

`m\angle LMN=104^(\circ)`

Therefore, the correct option is D.

Answer 2

104°

Explanation:

If segments NO and NM are congruent, then angles NMO and NOM are congruent. So, their supplements, angles NML and NOP are congruent. That is ...

∠NML ≅ ∠NOP = 104°

∠NML = 104°