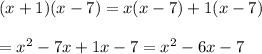Question

Which of the following is the product

Answer 1

`\text{\bf{A.}}\quad(3x^2)/(x^2-6x-7)`

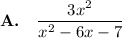
Explanation:

As with multiplying any rational expressions, the numerator of the result is the product of the numerators, and the denominator of the result is the product of the denominators.

`(3x)/(x+1)\cdot(x)/(x-7)=((3x)(x))/((x+1)(x-7))=(3x^2)/(x^2-6x-7)`

_____

The denominator product is found using the distributive property. Each of the terms of one factor is multiplied by the other factor.

`(x+1)(x-7)=x(x-7)+1(x-7)\\\\=x^2-7x+1x-7=x^2-6x-7`