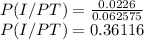Question

2.5% of a population are infected with a certain disease. There is a test for the disease, however the test is not completely accurate. 90.4% of those who have the disease test positive. However 4.1% of those who do not have the disease also test positive (false positives). A person is randomly selected and tested for the disease. What is the probability that the person has the disease given that the test result is positive?

Answer 1

`P(disease/positivetest) = 0.36116`

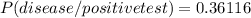
Explanation:

This is a conditional probability exercise.

Let's name the events :

I : ''A person is infected''

NI : ''A person is not infected''

PT : ''The test is positive''

NT : ''The test is negative''

The conditional probability equation is :

Given two events A and B :

P(A/B) = P(A ∩ B) / P(B)

`P(B) >0`

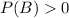
P(A/B) is the probability of the event A given that the event B happened

P(A ∩ B) is the probability of the event (A ∩ B)

(A ∩ B) is the event where A and B happened at the same time

In the exercise :

`P(I)=0.025`

`P(NI)= 1-P(I)=1-0.025=0.975\\P(NI)=0.975`

`P(PT/I)=0.904\\P(PT/NI)=0.041`

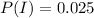
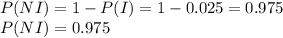
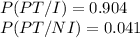
We are looking for P(I/PT) :

P(I/PT)=P(I∩ PT)/ P(PT)

`P(PT/I)=0.904`

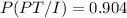
P(PT/I)=P(PT∩ I)/P(I)

0.904=P(PT∩ I)/0.025

P(PT∩ I)=0.904 x 0.025

P(PT∩ I) = 0.0226

P(PT/NI)=0.041

P(PT/NI)=P(PT∩ NI)/P(NI)

0.041=P(PT∩ NI)/0.975

P(PT∩ NI) = 0.041 x 0.975

P(PT∩ NI) = 0.039975

P(PT) = P(PT∩ I)+P(PT∩ NI)

P(PT)= 0.0226 + 0.039975

P(PT) = 0.062575

P(I/PT) = P(PT∩I)/P(PT)

`P(I/PT)=(0.0226)/(0.062575) \\P(I/PT)=0.36116`